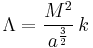Clearing the neighbourhood

"Clearing the neighbourhood of its orbit" is a criterion for a celestial body to be considered a planet in the Solar System. This was one of the three criteria adopted by the International Astronomical Union (IAU) in its 2006 definition of planet.[1]

In the end stages of planet formation, a planet will have "cleared the neighbourhood" of its own orbital zone, meaning it has become gravitationally dominant, and there are no other bodies of comparable size other than its own satellites or those otherwise under its gravitational influence. A large body which meets the other criteria for a planet but has not cleared its neighbourhood is classified as a dwarf planet. This includes Pluto, which shares its orbital neighbourhood with Kuiper belt objects such as the plutinos. The IAU's definition does not attach specific numbers or equations to this term, but all the planets have cleared their neighbourhoods to a much greater extent than any dwarf planet, or any candidate for dwarf planet.

The phrase may be derived from a paper presented to the general assembly of the IAU in 2000 by Alan Stern and Harold F. Levison. The authors used several similar phrases as they developed a theoretical basis for determining if an object orbiting a star is likely to "clear its neighboring region" of planetesimals, based on the object's mass and its orbital period.[2]

Clearly distinguishing "planets" from "dwarf planets" and other minor planets had become necessary because the IAU had adopted different rules for naming newly discovered major and minor planets, without establishing a basis for telling them apart. The naming process for Eris stalled after the announcement of its discovery in 2005, pending clarification of this first step.

Contents

Details

The phrase refers to an orbiting body (a planet or protoplanet) "sweeping out" its orbital region over time, by gravitationally interacting with smaller bodies nearby. Over many orbital cycles, a large body will tend to cause small bodies either to accrete with it, or to be disturbed to another orbit, or to be captured either as a satellite or into a resonant orbit. As a consequence it does not then share its orbital region with other bodies of significant size, except for its own satellites, or other bodies governed by its own gravitational influence. This latter restriction excludes objects whose orbits may cross but which will never collide with each other due to orbital resonance, such as Jupiter and the Trojan asteroids, Earth and 3753 Cruithne, or Neptune and the plutinos.[2]

In their paper, Stern and Levison sought an algorithm to determine which "planetary bodies control the region surrounding them".[2] They defined Λ (lambda), a measure of a body's ability to scatter smaller masses out of its orbital region over a long period of time. Λ is defined mathematically as

\Lambda = \frac{M^2}{a^\frac{3}{2}}\,k

where M is the mass of the body, a is the length of the body's semi-major axis, and k is a function of the orbital elements of the small body being scattered and the degree to which it must be scattered. In the domain of the solar planetary disc, there is little variation in the average values of k for small bodies at a particular distance from the Sun.[3]

If Λ > 1, then the body will likely clear out the small bodies in its orbital zone. Stern and Levison used this discriminant to separate the gravitionally rounded, Sun-orbiting bodies into überplanets, which are "dynamically important enough to have cleared its neighboring planetesimals", and unterplanets. The überplanets are the eight most massive solar orbiters (i.e., the IAU planets), and the unterplanets are the rest (i.e., the IAU dwarf planets).

Steven Soter proposed an observationally based measure µ (mu), which he called the "planetary discriminant", to separate bodies orbiting stars into planets and non-planets.[3] Per Soter, two bodies are defined to share an orbital zone if their orbits cross a common radial distance from the primary, and their non-resonant periods differ by less than an order of magnitude. The order-of-magnitude similarity in period requirement excludes comets from the calculation, but the combined mass of the comets turns out to be negligible compared to the other small Solar System bodies, so their inclusion would have little impact on the results. µ is then calculated by dividing the mass of the candidate body by the total mass of the other objects that share its orbital zone. It is a measure of the actual degree of cleanliness of the orbital zone. Soter proposed that if µ > 100, then the candidate body be regarded as a planet.

Here is a list of planets and dwarf planets ranked by Soter's planetary discriminant µ, in decreasing order.[3] Note that for all eight planets defined by the IAU, µ is orders of magnitude greater than 100, while for all dwarf planets, µ is orders of magnitude less than 100. Also listed is the Stern–Levison parameter Λ; again, the planets are orders of magnitude greater than 1, and the dwarf planets are orders of magnitude less than 1. The scattering power relative to Earth (Λ/ΛE) is also shown, as is the distance where Λ = 1 (where the body would change from a planet to a dwarf planet).

Rank Name Soter's Planetary
discriminant µ		 Stern–Levison
parameter Λ		 Mass (kg) Type of object Λ/ΛE Λ = 1 distance (au)
1 Earth 1.7 × 106 1.53 × 105 5.9736 × 1024 3rd planet 1.00 &100000000000028700000002,870
2 Venus 1.35 × 106 1.66 × 105 4.8685 × 1024 2nd planet 1.08 &100000000000021800000002,180
3 Jupiter 6.25 × 105 1.30 × 109 1.8986 × 1027 5th planet 8510 &100000000062200000000006,220,000
4 Saturn 1.9 × 105 4.68 × 107 5.6846 × 1026 6th planet 308 &100000000012500000000001,250,000
5 Mars 1.8 × 105 9.42 × 102 6.4185 × 1023 4th planet 0.0061 &10000000000000146000000146
6 Mercury 9.1 × 104 1.95 × 103 3.3022 × 1023 1st planet 0.0126 &1000000000000006000000060
7 Uranus 2.9 × 104 3.84 × 105 8.6832 × 1025 7th planet 2.51 &10000000000102000000000102,000
8 Neptune 2.4 × 104 2.73 × 105 1.0243 × 1026 8th planet 1.79 &10000000000127000000000127,000
9 Ceres 0.33 8.32 × 10−4 9.43 × 1020 1st dwarf planet 8.7 × 10−9 &100000000000000000245000.0245
10 Eris 0.10 2.15 × 10−3 1.67 × 1022 3rd dwarf planet 1.33 × 10−8 &100000000000000011299991.13
11 Pluto 0.077 2.95 × 10−3 1.29 × 1022 ± 10% 2nd dwarf planet 1.95 × 10−8 &100000000000000008120000.812
12 Makemake 0.02[4] 2.22 × 10−4 ~4 × 1021 4th dwarf planet 1.45 × 10−9 &100000000000000001680000.168
13 Haumea 0.02[4] 2.68 × 10−4 4.2 ± 0.1 × 1021 5th dwarf planet 1.72 × 10−9 &100000000000000001790000.179

Disagreement

Stern, currently leading the NASA New Horizons mission to Pluto, disagrees with the reclassification of Pluto on the basis that—like Pluto—Earth, Mars, Jupiter and Neptune have not cleared their orbital neighbourhoods either. Earth co-orbits with 10,000 near-Earth asteroids (NEAs), and Jupiter has 100,000 Trojan asteroids in its orbital path. "If Neptune had cleared its zone, Pluto wouldn't be there," he now says.[5]

However, in 2000 Stern himself wrote, "we define an überplanet as a planetary body in orbit about a star that is dynamically important enough to have cleared its neighboring planetesimals ..." and a few paragraphs later, "From a dynamical standpoint, our solar system clearly contains 8 überplanets"—including Earth, Mars, Jupiter, and Neptune.[2] Most planetary scientists understand "clearing the neighborhood" to refer to an object being the dominant mass in its vicinity, for instance Earth being many times more massive than all of the NEAs combined, and Neptune "dwarfing" Pluto and the rest of the KBOs.[3]

Stern and Levison's paper shows that it is possible to estimate whether an object is likely to dominate its neighborhood given only the object's mass and orbital period, known values even for extrasolar planets. In any case, the recent IAU definition specifically limits itself only to objects orbiting the Sun.[1]

See also

References

  1. ^ a b "IAU 2006 General Assembly: Result of the IAU Resolution votes". IAU. 24 August 2006. http://www.iau.org/public_press/news/detail/iau0603/. Retrieved 2009-10-23. 
  2. ^ a b c d Stern, S. Alan; and Levison, Harold F. (2002). "Regarding the criteria for planethood and proposed planetary classification schemes" (PDF). Highlights of Astronomy 12: 205–213, as presented at the XXIVth General Assembly of the IAU–2000 [Manchester, UK, 7–18 August 2000]. Bibcode 2002HiA....12..205S. http://www.boulder.swri.edu/~hal/PDF/planet_def.pdf. 
  3. ^ a b c d Soter, Steven (2006-08-16). "What is a Planet?". The Astronomical Journal 132 (6): 2513–2519. arXiv:astro-ph/0608359. Bibcode 2006AJ....132.2513S. doi:10.1086/508861. 
  4. ^ a b Calculated using the estimate for the mass of the Kuiper belt found in Iorio, 2007 of 0.033 Earth masses
  5. ^ Rincon, Paul (25 August 2006). "Pluto vote 'hijacked' in revolt". BBC News. http://news.bbc.co.uk/2/hi/science/nature/5283956.stm. Retrieved 2006-09-03. 

External links